PowerPoint on Reasoning Algebraically

PowerPoint on reasoning algebraically trying to get over the idea that you need to balance the left hand side of an equation with the right.

Equations, terms, expressions and identities are things that get mixed up all the time.
A term is something made up of numbers, letters or both and is found between operators such as add, divide, multiply and subtract or the equals sign. Examples of terms include x, 3y, xyz and 7. So when we say, collect the like terms, we are saying collect the numbers together, collect all the terms that have x in together etc. It is important to note that x terms and x squared are not like terms.
An expression is made up of several terms and does not include an equals sign. Examples of an expression might be 3x + 2, 6 - 7y etc. If you have an equals sign, you have an expression on the left hand side of it and another on the right.
An equation is something that contains an equals sign. A=B would be an equation where A and B are expressions.
An identity is denoted with a three bar equals sign. It means that something is always true, no matter what values are substituted for the unknown quantities. A simple example would be that 3x + 2 = 5x is true when x=1 and so this is an equation. 3x + 2x = 5x is always true, no matter what the value of x, so this is an identity.

PowerPoint on reasoning algebraically trying to get over the idea that you need to balance the left hand side of an equation with the right.

Form equations for the perimeter of rectilinear shapes and equate these to a given perimeter in order to find the unknown value.

Spreadsheet on balancing equations. Ideal for those students who find the concept a little more difficult as it gives them lots of arithmetic type practice to build up the concept. Originally written for my KS2 class.

Spreadsheet on balancing equations. Ideal for those students who find the concept a little more difficult as it gives them lots of arithmetic type practice to build up the concept. Originally written for my KS2 class.

Basic manipulation of equations introducing the idea of doing the same to the left hand side as you do to the right.

Plenty of examples and questions on changing the subject of an equation.

Plenty of examples on changing the subject of an equation which is self marked using the spreadsheet.

Forming equations to find the perimeter of ever more complex shapes. All the shapes are based on the rectangle.

Forming equations to find the perimeter of ever more complex shapes. All the shapes are based on the rectangle.
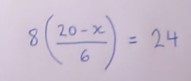
Video on finding the value of x by peeling away out the outer layers of an expression.

Examples of how to manipulate equations to find the unknown value in problems about perimeter.

Use the rule that opposite angles are equal in a parallelogram to find the size of the angles.

Information that would be useful to place on a maths display with a historical bend to it.

Varied worksheet on forming and solving equations using geometry as the backdrop.
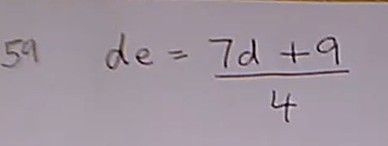
A video on Changing the Subject of an Equation including Factorising