Circle Theorem

Use the circle theorems to find the angles in a circle. A list of keywords is included and some sentences with cloze procedure.

The loci of a distance from a point is a circle. It describes a complete turn and allows us to work out many different things.
Important words to do with circles include centre, radius, circumference, diameter, tangent, chord, sector, segment and Pi.
The equation of a circle is x^2 + y^2 = r^2. If we alter it slightly, we get an elipse instead.
Circles are truely fascinating and we use them every day.

Use the circle theorems to find the angles in a circle. A list of keywords is included and some sentences with cloze procedure.

This is a difficult problem combining trigonometry, area of a circle, co-ordinates and midpoints to find the solution.

Two circles with the centre point marked. You can use this for all kinds of things. Naming the parts of a circle, find the area and circumference to name but a few.

A video about constructing a circle using the formula x^2 + y^2 = r^2 where r is the radius.

A face is given with dimensions upon it. You have to calculate the area of the skin by working out the areas of various circles, segments and sectors to find the final answer.
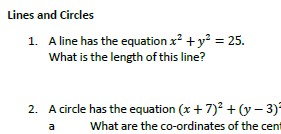
Use substitution in simultaneous equations to calculate the intersect points of a straight line and circle.
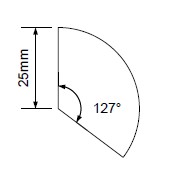
Find the area of a sector by finding the area of the fuill circle and then multiplying it by the angle at the centre of the circle divided by 360.
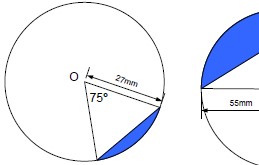
Problems on circles including area and circumference of a circle, perimeter and area of sectors, area of segments and a challenging exam question.

Print these off on single sided prints. Cut out the circle theorems and the diagrams to accompany them. Match them up and glue them into your book.