Video on Factorising Quadratics

In ax squared plus bx plus c, find the factors of c and then determine which ones will add up to make b.

A quadratic graph has the shape of a parabola. Be careful not to confuse it with graphs of higher orders of magnitude such as quartic graphs as these have a flatter base and steeper sides. All graphs whose highest order of index is even look like a U. That is, x to the power of 2, 4, 6, 8, 10, 12, 14,... etc look like a U but the higher the order, the flatter the base of the graph and the steeper the sides until, when you reach 100 or 200, it looks like the lower part of a square.
A quadratic equation is one where the highest index in the equation is 2. If the highest index is more than two, even if the equation contains an index of two, it is not quadratic.
When solving quadratic equations, we are looking for the roots or the solutions. These are the points where the graph line crosses the x axis ie, y=0. We can find these by two methods. Firstly, and more easily, by factorising the equation. However this does not always work. The other method is to solve the equation by using the formula. This does always work providing that there is a real solution. Remember that unless you enter the realm of complex numbers, there is no real solution to the square root of a negative number. Sometimes, there are no solutions to this type of problem. Sometimes, there is one solution but mainly, there are two.
Sometimes, we want to find the minimum point (right at the bottom of the graph). We can do this by using a method called completing the square. This will give us the co-ordinates of the least most point - the point at the bottom of the U.

In ax squared plus bx plus c, find the factors of c and then determine which ones will add up to make b.

In ax squared plus bx plus c, find the factors of c and then determine which ones will add up to make b.

Explanation of how to find the roots of a quadratic equation or graph. Includes completing the square identities.

Explanation of how to complete the square looking at the identities involved.

Factorise some quadratics to find the roots and then use the quadratic formula to find the roots of other quadratics if they exist.

In ax squared plus bx plus c, find the factors of c and then determine which ones will add up to make b.Solve these questions by factorising.

List of instructions for factorising a quadratic, completing the square and finding the y-intercept to sketch a graph.
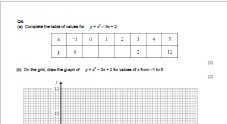
Exam Questions on Quadratics. Print pp1-12 for questions. Further pages include Examiners report and mark schemes
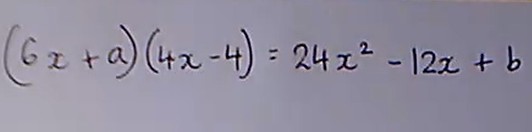
A video on expanding quadratics with unknown quantities
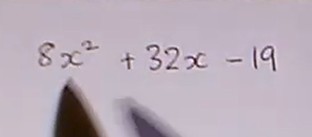
A video on Writing a Quadratic in Completed Square Form